Los finales de peones son aparentemente sencillos en su forma o apariencia sobre el tablero de ajedrez, pero desde luego no lo son en su contenido. Los conceptos y maniobras que dirigen el cálculo de este tipo de finales no son obvios ni de sentido común, incluso en algunos momentos resultan paradójicos y contradictorios (por ejemplo, en algunas posiciones es bueno ganar tiempos y en otras perderlos).
En este artículo pretendemos explicar algunos de los conceptos ajedrecísticos que hay que conocer a la hora de enfrentarse a un final de peones, posteriormente el lector deberá profundizar en ellos realizando ejercicios y resolviendo problemas de finales de peones.
Maniobras del rey
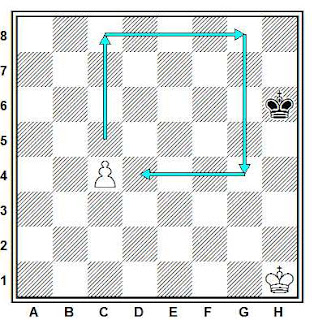
El rey (ver diagrama superior) puede acudir de e1 a e8 en siete jugadas utilizando un total de 392 caminos diferentes, esto es debido a la geometría del tablero. Sin embargo para ir de e1 a h4 el camino más corto se corresponde con la diagonal e1-f2-g3-h4. La cuestión es que en muchos finales de peones, la clave de la victoria se encuentra en realizar un avance en zigzag en lugar de desplazar el rey en horizontal o vertical.
Cuadrado del peón
Este concepto sirve para calcular si un rey puede detener un peón libre antes de que llegue a su casilla de coronación. El concepto consiste en dibujar un cuadrado imaginario donde uno de los lados esté formado por las esquinas constituidas por el peón y su casilla de coronación. Si al jugar el rey entra dentro de dicho cuadrado, entonces podrá detener el peón, no pudiendo hacerlo en caso contrario.
No obstante, el ejemplo del diagrama inferior es un caso especial por encontrarse el peón en su casilla de origen y poder en este caso avanzar dos casillas en lugar de una, por lo que el cuadrado debe formarse una casilla por encima del peón. En la posición de ese diagrama, si juega el blanco gana y si mueve el negro son tablas.
Casillas críticas de f6
Estas casillas son e7 y g7. Naturalmente para las casillas c6, d6 y e6, las casillas críticas son las casillas equivalentes. Sin embargo cuando los peones están en a6, b6, g6 y h6 se encuentran bajo el efecto “borde del tablero” del que hablaremos más tarde.
En nuestra posición ejemplo, los reyes se disputan la casilla crítica g7. Si le tocase mover al negro este se puede “oponer” jugando 1… Rg8, controlando g7 y evitando la coronación. Por contra si mueve el blanco, este solo tiene que jugar 1. f7 para ganar (1… Re7 2. Rg7 y el peón corona).
La regla general en estos casos es que un peón no gana si llega a la séptima fila dando jaque, por contra gana si no da jaque (obviamente esto es válido cuando no hay más material sobre el tablero).
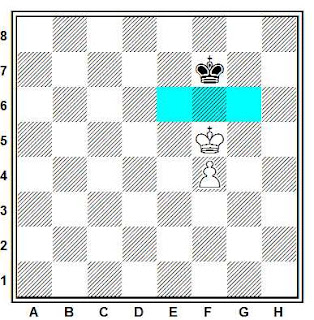
Casillas críticas de f5
Dichas casillas son e6, f6 y g6, de manera que si el rey blanco ocupa cualquiera de ellas el peón coronará sin remedio. Por lo tanto, en el ejemplo del diagrama e independientemente de quien juegue, siempre ganará el blanco ya que una de las casillas críticas está ocupada por su rey.
Casillas críticas de f4
Las casillas críticas del peón en la cuarta fila son exactamente las mismas que las del peón en quinta, es decir, e6, f6 y g6. En la posición del ejemplo los reyes luchan por controlar dichas casillas de manera que al que le toque mover perderá el control de alguna de ellas. Por lo tanto, si mueve el negro pierde, al tener que ceder e6 o g6 al contrario (1… Rg7 2. Re6 o 1…Re7 2. Rg6), y si mueven las blancas son tablas por el mismo hecho (1. Rg5 Rg7 y el rey blanco no podrá ocupar nunca las casillas temáticas sin avanzar el peón).
Resulta importante señalar que si el peón blanco estuviese en f3 o en f2, entonces el blanco gana independientemente de quien mueva ya que las negras deberán ceder en algún momento las casillas críticas… un buen ejercicio es que lo comprobéis.
Concepto de oposición
Se dice que hay oposición cuando los reyes están situados uno en frente del otro, en línea recta o en diagonal con un número impar de casillas entre ambos. Cuando solo existe una casilla entre ambos se denomina oposición inmediata, si hay tres o cinco nos encontramos ante una oposición distante.
Efecto borde el tablero
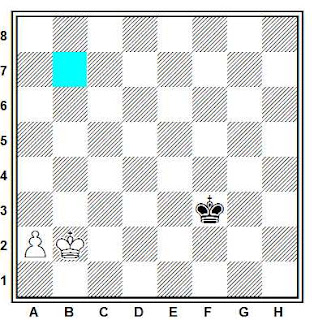
En el ejemplo del diagrama, el blanco necesita ocupar b7 para apoyar su peón, pero si es el negro el que mueve este llega a c6 defendiendo b7 y consigue tablas. En cambio el blanco gana si es este bando el que mueve ya que el negro no puede evitar que ocupe la casilla b7.
En este otro ejemplo no existen dos casillas crítica, sino que solo es crítica la casilla h7 y es esta la casilla que los reyes deben disputarse.
Si el blanco mueve para ganar debe jugar 1. Rh6! Rh8 2. g6 Rg8 3. g7 y el peón termina coronando. Por contra si juega 1. Rf6? Rh7 2. Rf7 Rh8 3. Rg6! se vuelve a la posición inicial sin haber realizado ningún progreso (afortunadamente el blanco todavía está a tiempo de jugar Rh6, no obstante si hubiera jugado 3. g6?? el resultado sería tablas por rey ahogado).
Cuando hay más elementos sobre el tablero, ya sean peones o piezas, el borde del tablero es muy peligroso para el rey que lo ocupa, algo que se puede comprobar en algunas posiciones donde ambos bandos coronan simultáneamente.
Ganancia de tiempo
La ganancia de tiempo es un concepto decisivo en los finales de peones. Se trata del número de jugadas que podemos hacer (tiempos) sin tener que mover nuestro rey. Si en un final de peones podemos ganar algún tiempo con respecto a nuestro contrario, nuestras probabilidades de ganar aumentarán al tener más posibilidades de forzar la oposición.
Veamos como debe proceder el negro en las siguientes posiciones para no perder tiempos (ojo, este es un ejemplo de cómo evitar que el blanco gane un tiempo, pero no quiere decir que perder dicho tiempo lleve a la derrota en las posiciones de los diagramas):
1. a3 a6 (1… a5? 2. a4 y el blanco gana un tiempo) 2. a4 a5.
1. a3 a6 2. b3 b6 3. a4 a5.
1. a3 a6 2. b3 b6 3. c3 c6 4. a4 c5! (4… a5? 5. b4! c5 6. bxc5 bxc5 7. c4 con ganancia de tiempo) 5. b4 c4! 6. b5 a5.
En el ejemplo anterior podemos observar que un cambio supone una pérdida de tiempo.
Triangulación del rey
La triangulación del rey se trata de una pérdida deliberada de tiempo con objeto de ganar la oposición.
En el ejemplo del diagrama la triangulación y pérdida de tiempo se completaría de la siguiente manera: 1. Re5! Rf8! 2. Rf4 Rg8 3. Re4! Rf8 4. Re5! Rf7 5. Rf5, llegándose a la misma posición inicial pero siendo el negro el que mueve, por lo que la partida está perdida para este bando al tener que ceder la oposición y poder el blanco ocupar la casilla g6 capturando el peón negro a continuación.









0 comentarios:
Publicar un comentario