Clasificación del Problema de Ajedrez (II) - Problemas Directos

En los problemas de mate directo es el enunciado el que determina el número de jugadas en que este debe llevarse a efecto. Su enunciado es el siguiente:

Las blancas dan mate en “N” jugadas

N, puede tener cualquier valor aritmético positivo, aunque los de más de 5 jugadas han sido muy escasos. Los de 4 y 5 jugadas, frecuentes en los países sajones, han ido decreciendo en las últimas décadas, siendo hoy muy escasos los autores que incluyen en su producción este tipo de obras.

P. H. Williams
Birmingam News, 1897
MATE EN 2
(4 + 2)

Los de mate en 2 y 3 jugadas son los grandes protagonistas y, precisando un poco más, habrá que decir que los de mate en 2 son el auténtico “Buque Insignia” del mundo de la composición. En ellos se ha volcado toda la capacidad de composición del ser humano, al tiempo que las mayores bases de datos dedicadas a recogerlos y ordenarlos, rivalizando en capacidad para albergar los cientos de miles de ellos que dormitan entre las memorias de silicio.

Existen dos detalles muy especiales sobre la posición inicial de este tipo de problemas, y que son ciertamente curiosos. Se trata del consenso mundial al que se ha llegado sin determinación ni imposición alguna sobre el que sean las piezas blancas las que llevan a cabo tanto la jugada inicial o clave, como la ejecución de los mates, dejando solamente para las piezas negras la defensa de la amenaza que genera dicha clave y en los problemas de modalidad de ataque. En los de bloqueo, la actuación negra se limita a ser una especie de simple comparsa al servicio exclusivo de la creación de variantes para el enriquecimiento del problema. Esta prerrogativa blanca parece haber sido influenciada por el mismo protagonismo que este bando tenia adquirido para el inicio de la partida de ajedrez, echo que también queda reflejado en el sentido del movimiento de los peones. Es decir, si el tablero lo tomamos como referencia vertical, los peones blancos ascienden y los negros lo hacen a la inversa.

El otro detalle especial hace referencia al consenso generalizado de no admitir una determinada posición inicial si esta no puede ser obtenida bajo el desarrollo normal de una partida jugada por dos jugadores.

Por esta circunstancia se permiten posiciones totalmente inverosímiles y rocambolescas, pero no aquellas que denotan imposibilidad. Tampoco son admisibles posiciones iniciales con dos damas, tres torres, tres alfiles, tres caballos, dos alfiles que circulen por casillas del mismo color, o más de los 8 peones. Estas posiciones solo son aceptadas si durante el transcurso del problema son fruto de promociones de peones en la octava fila.

Cualidades exigidas a un problema directo

Las cualidades exigidas en los problemas directos son varias.

Hay dos que son excluyentes si existiese transgresión a las mismas. Estas cualidades son Originalidad y Corrección.

Originalidad. Una obra es original o no lo es. Si un problema presenta la misma clave y desarrollo de los mates que otro editado con anterioridad, el problema es nulo y considerado “Anticipado”, palabra que sustituye a otra más dura como la de “Plagio”, y ello en aras de la posibilidad de que se haya producido una coincidencia bajo las leyes que rigen la combinatoria y la teoría del azar en el cálculo de probabilidades.

M. Havel
Romanleser, 1900
MATE EN 2
(4 + 2)

Nils G. C. Van Dijk
Problemisten, 1954
MATE EN 2
(4 + 2)

Como se puede observar, la primera composición de Williams, que podemos ver al principio del artículo, fue “a posteriori” doblemente “Anticipada”.

La segunda de Havel es idéntica a la de Williams, solo difieren por un giro de 90º. Y la tercera, la posición de Van Dijk, es respecto a la de Havel un cambio de simetría con eje vertical entre la 4ª y la 5ª columna, o también la imagen especular o reflejada por un espejo.

La solución al problema de Williams es:

La clave 1.Td2 (Bloqueo), y ahora si:

1…Ab4 2.Da7++
1…Ra5 2.Td6++
1…Rc5 2.Dd4++
1….Rc7 2.Dxa5++

La clave de Havel es 1.Tg4 y la de Van Dijk 1.Tb4.

Los desarrollos del resto de jugadas son lógicamente idénticos y solo cambia la nueva nomenclatura de las casillas. Lo paradójico de este caso es el hecho de que algunas bases de datos siguen ajenas, todavía hoy, de estas “Anticipaciones”, y desfilan por sus memorias cual si estuviesen aún vivos, e incluso en la popular obra 2345 Problemas de Ajedrez del prestigioso Chess Informator de Belgrado, en su última edición consultada, aparecían rebosando de buena salud. Como este caso existen otros muy numerosos, algunos con cinco “Anticipaciones” o más. Hoy día los jueces de un concurso de problemas inéditos, tienen a su alcance los instrumentos necesarios para detectar y anular estas lamentables anomalías. En la mayoría de los casos estas “anticipaciones” son el fruto del agotamiento de las ideas y suelen ocurrir con más frecuencia en problemas con pocas piezas. Incluso, a veces, son el nítido reflejo de un tema que quedó archivado en la memoria y un día y de forma involuntaria se materializa en el tablero.

Por otro lado conviene remarcar que sí se considera original la realización de una idea anterior compuesta con elementos nuevos y distintos que tienden a mejorar o equiparar esta idea.

Corrección. La otra cualidad excluyente es la corrección. Solo existen dos opciones, un problema es correcto, o no es correcto.

Las causas que condicionan la corrección son varias. Veamos:

Por el enunciado. Cuando no pueda cumplirse el enunciado por:

• No se puede dar mate en el número de jugadas que promulga el enunciado. Normalmente debido a una jugada de defensa negra no prevista por el autor. El problema recibe el nombre de insoluble.
• Cuando existan otra o más claves (primeras jugadas), no previstas por el autor, o si se puede solucionar en un número de jugadas inferior al señalado por el enunciado. Se denominan entonces como falsos o inexactos.

Por la disposición de las piezas en el tablero. Es válido aquí lo mencionado sobre la obligación de que la posición inicial ha de ser posible por el juego de una partida entre jugadores, así como lo dicho sobre el número de tres o más piezas iguales, y añadiremos también como de obligación “sine qua non” que el número de capturas realizadas por los peones para justificar su posición sea concordante con el número de piezas existentes del bando contrario en la posición inicial. Por último, el problema, como consecuencia de que las blancas hacen la primera jugada, ha de tener en cuenta la pregunta siguiente: ¿Cuál o cuáles pudieron ser las inmediatas anteriores jugadas de las negras?

Lo mencionado como cualidades exigibles en Originalidad y Corrección se hace extensible a cualquier otro tipo de problema con la excepción de los llamados de Multi-Solución.

Posiciones imposibles

Veamos algunos ejemplos de posiciones imposibles que se reflejan en el diagrama anterior:

• En el cuadrante superior izquierdo contemplamos la posición de tres peones negros que resulta imposible en una partida.
• En el cuadrante superior derecho la posición del alfil negro es imposible, ya que no pudo salir de su casilla inicial por que los peones negros se mantienen en sus casillas de origen.
• En el cuadrante inferior izquierdo la ilegalidad la representa el apoyo del alfil a su peón desde una casilla a la que no pudo acceder jamás.
• Por último en el cuadrante inferior derecho, vemos dos torres blancas. Una de ellas puede ser la del ala de dama, pero la otra ha de ser la de rey, y su posición es netamente ilegal, ya que nunca pudo evadir el encierro al que le someten el alfil y los peones propios.

Teodore M. Brown
British Chess, 1855 (?)
MATE EN 2
(8 + 7)

La solución es:

1.Db8 (Bloqueo), y ahora si:

1…Rb5 2.Ad3++
1…Rb3 2.Ca6++
1…Rd5 2.Pc4++
1…Rb4 2.Dg8++

Magnífica composición. Excelente clave. Generosidad en variantes. Bellos temas estratégicos. Sorprendentes mates. Pero fatalmente el problema está “debatido”, es decir Nulo. Su causa radica en la posición de los peones negros, los cuales sugieren que han tenido que realizar diez capturas para justificarla, y debido a ello solo podrían quedar seis piezas blancas en esta posición, y contamos ocho.

W. A. Shinkam
Deuches S., 1875
MATE EN 2
(4 + 4)

La solución es:

1.De6 (Bloqueo), y ahora si:

1...exd6 2.Df6++
1…fxe6 2.Ae5++
1…h5 2.Dh6++
1…h6 2.Dxh6++

En la clave se añade el sacrificio de la dama al ya inicial del alfil. Las blancas carecen de más piezas pero sin embargo vencen de forma brillante. Una gran idea perfectamente realizada, pero al igual que la anterior composición, a esta hay que demolerla por otra razón. No se puede contestar a la pregunta cuál fue el último movimiento de las negras, ya que no pudieron jugar absolutamente nada.

Debemos mencionar como curiosidad que estas dos últimas composiciones, como algunas otras, figuran vivas en varias bases de datos muy prestigiosas. Por ejemplo, figuran en la base argentina Snieder, respectivamente con los números 17.001 y 115.596, en la que es la última actualización consultada a 1 de enero de 2016.

Las restantes cualidades del problema directo con carácter no excluyentes son: Dificultad, Variedad, Economía y, por último una especie de simbiosis, que en extraño maridaje se recrean las ideas y la acción del problema, y a las que conocemos respectivamente como Belleza y Elegancia, que resumiríamos bajo una sola palabra: Arte.

Dificultad. Es una cualidad que realza enormemente el valor global del problema. Una clave altamente “Grosera” puede llegar a arruinar el conjunto de una buena obra. Así una clave con jaque al rey negro, o con captura de una pieza de este color, o que tenga valor restrictivo sobre los movimientos del rey negro, no son aceptables por si mismas.

La clave ha de desconcertar al solucionista. Debe ser todo lo sorprendente que sea posible, o ser un poco ilógica, y deberá en lo posible realizarse mediante jugadas que, aparte de inesperadas, aparenten ser inocuas o inofensivas o hasta perjudiciales para el logro del mate. Realza la dificultad el acto de situar las piezas con gran libertad, al objeto de aumentar el número de jugadas a meditar y ensayar.

Evidentemente un problema en tres jugadas debe de ser más difícil que uno de dos, y uno de cinco lo ha de ser más que uno en tres. Pero el concepto de Dificultad es, como todas las cosas, un tanto relativo a la capacidad innata de un solucionista determinado, y a su particular especialización en un específico tipo de problema o número de jugadas.

J. A. López Parcerisa
SEPA “80”, 2014
4ª Recomendación
MATE EN 3
(6 + 6)

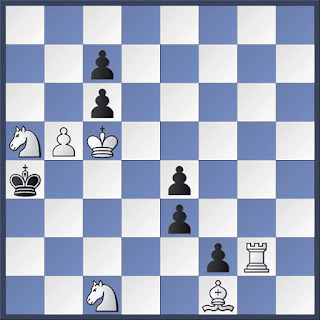
En el diagrama precedente podremos observar varios detalles de la temática que acabamos exponer.

La solución es:

1.Ae2 (Bloqueo), y ahora si:

1…f8D 2.Ad1+ Rxa5/Ra3/Dxd1 3.Ta2++
1…Rxa5 2.Tg8 Negras juegan 3.Ta8++
1…Ra3 2.Cc4+ Ra4 3.Ad1++
1…cxb5 2.Axb5+ Ra3 3.Cc4++

Podemos ver en este Meredith, (12 piezas), como su nivel de dificultad ha aumentado un poco, pero muy lejos del carácter de tipo exponencial que concedía Sam Loyd al aumento de la dificultad entre problemas de mayor número de jugadas. La clave es inocua e imprevista y permite la inmediata coronación negra. Buena variabilidad y Economía de piezas, participando todas ellas en alguno de los mates. La posición de mate de la última variante es conocida como mate Musset.

Variedad. Tras de la primera jugada de las blancas conocida como Clave, las piezas negras han de jugar, tal como es preceptivo según la ley de alternancia de jugadas, y cada respuesta negra que obligue a las blancas a jugar de un modo distinto, produce una variante. Así pues, habrá tantas variantes como segundas jugadas blancas diferentes existan en una composición. La variante o variantes donde se plasma la idea que promueve la composición se denominan principales o temáticas, y las restantes serán las complementarias o juego adjunto.

Las variantes complementarias han de surgir de un modo natural del eje del problema, por lo tanto se consideraban un defecto todas aquellas que eran forzadas o artificiales, pero la escuela inglesa y norteamericana, muy tolerantes en este aspecto, han influido poderosamente en su aceptación y sobretodo en los problemas de mate en 2 jugadas. Una idea escueta denota hoy día falta de habilidad de composición.

Los compositores de nuestra época, al no serles exigible como antaño la economía y la pureza de los mates, pueden extender sus capacidades hacia el aumento de variantes y otras exigencias de la composición actual. El incremento de variantes se logra mediante el aumento de piezas negras que se opongan a la amenaza de la clave, pero lo que no debe incrementarse es el número de piezas blancas para ser utilizadas en tan solo una variante, sobre todo si se trata de una pieza "pesante" o poderosa como la dama o la torre.

Ha ganado, en este último siglo, una extraordinaria relevancia el llamado juego virtual o juego aparente, que viene a ser lo que podría suceder, si no fuese porque lo impide algún condicionante, lo cual obliga a buscar y ahondar más en el problema, y en algunos casos los mates de los juegos virtuales reaparecen como jugadas en el juego real. Este apareamiento entre el juego virtual y real, engrandece y enriquece poderosamente la brillantez de una composición.

Hoy en día se contempla como norma habitual que un problema directo en dos jugadas presente de 4 a 6 variantes en total y en problemas de ataque. En los de tres jugadas, de tres a cuatro y descendiendo para problema de mayor prolongación. En las composiciones de bloqueo se exige más variantes que en los de ataque. Todo ello bajo una norma no escrita y creada por el buen uso y costumbre en el terreno internacional.

Uno de los problemas de mate en dos, que conocemos con más variantes es el que exponemos seguidamente:

H. F. Meyer
Sber Land, 1860 (?)
MATE EN 2

Su clave es 1.Td4d3 bloqueo.

El resto de las variantes y los respectivos mates los encontraremos “más adelante”.

¿Cuál es el motivo? -se preguntará el lector.

Existe un especial detalle para reservar por el momento estas jugadas. Por una parte, el lector podrá practicar la búsqueda de los mates respectivos que se producen y, por otra, intentaremos utilizarlos en la descripción de un nuevo tipo de problema, ya que este gran número de variantes es difícil de reencontrar. Si, anticiparemos que el autor describe: !Un total de 19 Variantes y cuadros de mate distintos¡

Economía. Economía en un problema no significa componerlo con pocas piezas, significa realizarlo con las piezas justas, sin que sobre nada superfluo o absolutamente necesario. Se aceptan piezas de poco peso que ayuden a la corrección evitando dobles soluciones de clave o duales. También debe entenderse la economía como condicionante de la fuerza empleada, de tal modo que si para un efecto determinado basta un peón, no colocar un alfil o una fuerza superior a la mínima necesaria.

A principios del pasado siglo, la restrictiva escuela germánica exigía que la economía se extendiese hacia la obligación, que la variante principal debía concluir con un mate puro y económico. El mate económico es aquel en el que todas las piezas blancas supervivientes, excepto rey y peones, colaboran activamente en el mate. Un mate es puro cuando las 8 casillas que rodean al rey negro están dominadas por una sola pieza blanca u obstruida por una pieza negra, pero sin dominio blanco. Cuando el mate es a la vez puro y económico se conoce como mate Perfecto o mate Reglamentario.

La observación estricta de este precepto alemán limitaba de forma importante la producción de problemas en pocas jugadas, por lo que no debe extrañar que los grandes compositores fueran abandonando las obligaciones de tan estrecho canon en beneficio de una mayor libertad de composición, que se plasmaba en el mejoramiento de la calidad de las combinaciones y del realce de la belleza de las ideas.

Utilizar piezas importantes de cualquier color para asegurar la corrección, sin que influyan directa o indirectamente sobre el rey negro en ningún momento de la solución, viola gravemente la esencia de la economía, por lo que es esencial la búsqueda de otros métodos para lograr el mismo efecto.

Como en todas las reglas existen excepciones, por ello traemos un ejemplo de violación a la regla que impide que en el problema coexista alguna pieza innecesaria. Veamos como Sam Loyd se saltó esta regla en beneficio de esta composición que fue altamente premiada.

Samuel Loyd
American Problem, 1878
1º Premio
MATE EN 2
(12 + 7)

La solución es:

1.Tf5 amenazando 2.Da4++

Si 1…Rxb3 2.Cc5++
1…Tb3 2.Cg5++

Es sencillo comprobar, que si de la posición original quitamos el peón de f3, la solución del problema es exactamente la misma. Entonces, ¿por qué situar este peón? Loyd lo hizo así por una razón de peso. Sin este peón, un solucionista vería rápidamente que las negras tienen la defensa 1…Tc1+, la cual invalidaría el mate, y consecuentemente buscaría una clave que impidiera la acción de la torre negra y llegaría prontamente a descubrir la clave con un mínimo esfuerzo. La posición de este peón engrandece una de las cualidades de la composición, que es la Dificultad. Y con ello se embellece el problema.

El propio Sam Loyd escribió (según se incia en la Enciclopedia del Ajedrez):

“… todo el mérito de esta composición se apoya en la magistral inactividad de este pequeño intruso... soy deudor a este peón del 1ª premio con el que fue recompensado el problema.”

Cuando no quede más remedio que quebrantar la exigencia de la Economía, deberá hacerse mediante la utilización del elemento, el cual la infrinja en su mínima expresión.

Belleza y Elegancia. Esta última exigencia de las composiciones de mate directo es la más subjetiva y, por ello, la de más difícil valoración y concreción. Estos elementos presentan un carácter indivisible. Son como dos aspectos de una misma cosa contemplados desde diferentes perspectivas. Tal vez un buen símil podría ser la propia “luz”, la cual se nos presenta de forma “bi-faz”, a veces como onda y otras como partícula crepuscular.

Son, pues, el fondo y la forma de una misma cosa, de un mismo elemento, en donde el fondo es la evolución artística, y la forma es la disposición de las ideas para su realización, de tal modo que generalmente se acuña el término de elegancia a la ejecución y desarrollo del problema, y la belleza a la idea generatriz de todas las partes de la composición.

Podríamos citar como elementos de la elegancia y belleza:

• Una clave con un movimiento imprevisto y aparentemente inocua.
• Una posición natural que propicie movimientos con recorridos largos, sin agrupaciones, armónica en su conjunto y bien centrada que destile naturalidad.
• Utilizar el menor número de piezas sin detrimento de la idea producirá una mayor esbeltez.
• Cuadros de mate que sean o tiendan a parecer mates “Espejo”, (del ingles “Mirror”). Es decir que el rey negro parezca en su posición de mate disfrutar de una libertad o espacio inexistente.
• Claves que liberen casillas de fuga, sacrificios, …

Deseamos antes de poner fin a este apartado de mates directos, recordar que los problemas de bloqueo incompleto han caído en desuso, salvo raras excepciones. Sí persisten aquellos que en su posición inicial presentan un bloqueo total, o sea aquellos en los que la clave es una jugada de espera muy especial, o la clave cambia al menos alguno de los mates previstos y que son conocidos también bajo la denominación de Mutate.

Veamos un problema en donde una pieza, en este caso un caballo negro, realiza la actuación de máximo efecto dibujando una rueda, conocida como el tema de la “Rosa Negra”.

H. Heathcote
H. & H. Express, 1905
1º Premio
MATE EN 2
(10 + 1)

La solución es:

Clave 1.Tc1c7 amenazando 2.Cc3++ y en el juego principal, a cada movimiento defensivo del caballo negro, de los 8 en total, corresponde un mate determinado y distinto.

Veamos a continuación un problema de Mutate. Este término fue acuñado por primera vez gracias a este problema que fue presentado al Congreso Ajedrecístico de Estados Unidos, sección Meredith de 1921.

Brian Harley y C. Promislo
Congreso USA - Meredith, 1921
3ª Mención de Honor
MATE EN 2
(5 + 4)

El problema especula con el tema de las semi-clavada de caballos negros, tanto en los mates previstos como en los que surgen tras de la ejecución de la clave.

Los mates previstos antes de jugar la clave son:

Si 1…Cg8 2.Dg8++
1…Cb juega 2.Dc8++
1...Cd juega 2.Dd5++

Tras la clave 1.Dc7 aparecen nuevos mates:

Si 1…Cd5 2.Dc8++
1…Cb juega 2.Dc4++
1…Cd juega 2.d5++

Sin menosprecio a otro tipo de composiciones, algunos de ellos muy interesantes, podemos afirmar que los problemas directos de mate en dos jugadas han sido y seguirán siendo la capilla Sixtina del culto a la composición ajedrecística.

José Antonio López Parcerisa
Miembro de la SEPA
Sociedad Española de Problemistas de Ajedrez

Artículo anterior: Clasificación del Problema de Ajedrez (I)